Lehetőségelemzés

2. Solver

A Solver az Excel egyik legtöbbet használt bővítménye, tehát eredetileg csak passzív része a programnak. Így, ha használni szeretnénk, előbb be kell töltenünk. Ennek lépéseiről - sőt a funkció használatáról is, az itteninél bővebben - remek leírás olvasható a Microsoft honlapján.

A funkció nagyon hasonlít az előbb tárgyalt célérték-kereséshez, hiszen ugyanolyan típusú problémák megoldására való, csak éppen több beállítási lehetőséggel rendelkezik. Így minden célérték-kereséssel megoldható probléma megoldható Solverrel is, egyes esetekben viszont csak a Solver nyújt segítséget.

Nézzük, mely szempontok alapján egyezik meg a két funkció:

• Meg kell adni egy cellát, ahol az eredményt szeretnénk megkapni.
  Ennek célérték-keresésnél Célcella, Solvernél Célkitűzéscella nevet adtak. Természetesen képletet kell tartalmaznia.
• Meg kell adni az értéket, amit az előbbi cellában szeretnénk kapni.
  Célérték-keresésnél ezt hívjuk célértéknek, a Solver pedig egyszerűen csak célként hivatkozik rá.
• Meg kell adni, hogy mely cella tartalmát módosítsa ennek érdekében.
  Célérték-keresésnél módosuló cellának, Solvernél változócellának hívjuk. Közvetve vagy közvetlenül kapcsolódnia kell a cél(kitűzés)cellához.
• A megoldási módszer mindkét esetben a próbálgatás, így nem biztos, hogy pontos értéket kapunk, vagy, hogy egyáltalán van megoldás.
• Az eredmény természetesen nem adatkövető.

A következő képernyőkép az eszköz használatát mutatja be, megjelölve az előbb is említett paramétereket. Habár ez nem teljesen szakszerű, az összhang megőrzése érdekében maradnék a célérték-keresésnél megszokott kifejezéseknél. A mellékelt feladatmegoldásoknál is ugyanezt a színezést használom, hogy könnyebb legyen összevetni azokat a leírással (persze kék színezést ne keressen senki). Gyakran előfordul, hogy a módosuló cellákra korlátozás is vonatkozik, ezért döntöttem úgy, hogy a narancssárga színt kitöltésre, a pirosat betűszínezésre használom, lehetőséget biztosítva így egy cella két színnel történő megjelölésére.

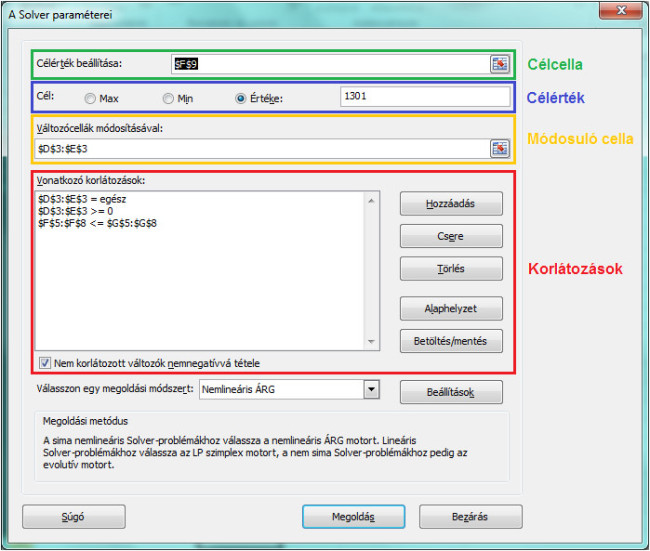A kép (nagyobb változata) külön ablakban is megtekinthető.72_full.jpg72. ábra: A Solver ablaka, megjelölve benne a legfontosabb részek.

Nézzük meg azt is, miben különbözik a Solver a célérték-kereséstől:

• Célértéknek nem csak egy konkrét szám adható meg, hanem az is, hogy a célcella értéke legyen minimális vagy éppen maximális.
• Akár több, de maximum 200db módosuló cellát is megadhatunk, vesszővel elválasztva.
• Megadhatóak úgynevezett korlátozások is, vagyis hogy mely kikötések mellett kívánjuk a célunkat elérni. Egy korlátozáshoz meg kell adni a cellatartományt és a feltételt. A feltételben a ≤, =, ≥ relációs jelek vagy az int (egész), bin (bináris) és dif (mind különböző) kulcsszavak valamelyike használható.

Látható, hogy a Solver használatának megértése nem is olyan nagy lépés a célértékkeresés ismerete mellett. Még sincs egyszerű dolgunk: a feltételek megfogalmazása, és annak olyan formába öntése, amit a Solver is megért, gyakran nem kis feladat. A funkció rutinszerű használatának képessége rengeteg gyakorlást, kreativitást igényel!

Nézzünk meg előbb egy egyszerűbb, majd egy nehezebb példát!

A feladat így szól: "Meghívtuk tizennégy ismerősünket vendégségbe. Kétféle szendvicset tudunk csinálni:

• sonkásat (3dkg vaj, 3dkg sonka, 2dkg sajt, negyed tojás)
• sajtosat (2dkg vaj, 1dkg sonka, 5dkg sajt, fél tojás).

Kenyérből bármennyi a rendelkezésünkre áll, de a többi alapanyagból csak korlátozottan: 120dkg vaj, 100dkg sonka, 200dkg sajt, 20db tojás.

• a) Készítsük el a lehető legtöbb szendvicset! Hány sonkásat és hány sajtosat tudunk majd felkínálni?
• b) Úgy döntöttünk, hogy a szendvicseket inkább pénzért adjuk, hogy a bevétellel kompenzáljuk az egyéb kiadásokat. A sonkáson darabonként 40, a sajtoson darabonként 31Ft-ot tudunk keresni. Mennyi lehet a maximális haszon?
• c) Mennyi lesz a minimális haszon, ha legalább annyi szendvicset kell csinálnunk, mint ahányan leszünk?
• d) Hány sajtos és sonkás szendvics készült, ha mindet eladtuk, és pontosan 1301Ft lett a nyereség?".

Az ilyen feladatoknál mindig az a legnehezebb, hogy kitaláljuk, milyen formában rögzítsük az adatokat, hogy aztán könnyedén megfogalmazhassuk a feltételeket. Szerencsére most nincs nehéz dolgunk, ráadásul a négy feladat erőteljesen hasonlít is egymásra, így elég egyszer kitalálnunk az elrendezést, és aztán munkalapmásolással előkészíteni a helyet mindegyik feladat megoldására.

• Rögzítsük az adatokat az alábbi formában! D5:F9, valamint C12 számolt cellák, készítsük el a képleteket is! Ha végeztünk, másoljuk a munkalapot még három példányban, hogy mind a négy feladat külön munkalapon legyen!

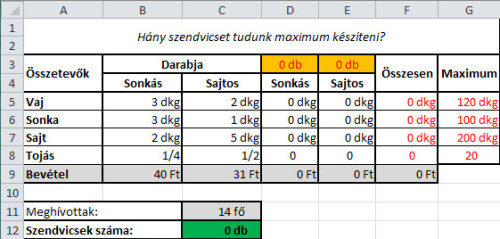A kép (nagyobb változata) külön ablakban is megtekinthető.73_full.jpg73. ábra: Az a) feladathoz tartozó munkalap. Szürke kitöltése azoknak a celláknak van, amikre ennél a feladatnál nincsen szükség.

Az a) feladat megoldása következik.

Az ábra sokatmondó: C12-be szeretnénk kiszámolni, maximum hány szendvics készíthető el. Ehhez D3 és E3 értékeit kell próbálgatni, miközben figyelünk arra, hogy ne lépjük túl a G5:G8-ban rögzített maximális mennyiségeket, és ne adjunk meg életszerűtlen adatokat.

• Válasszuk az Adatok/ Solver gombot, és töltsük ki az ablakot az alábbiak szerint:

Az eredményt gyorsan megkapjuk: 50db szendvics készíthető ennyi alapanyagból. Ennél jóval többet is megtudhatunk, ha a megoldás megtalálásakor nem csupán elfogadjuk azt, hanem kérünk egy jelentést is:

• Az OK-ra kattintás előtt válasszuk a Jelentések/ Eredmények opciót!

Így egy generált munkalapon olvashatjuk a megoldás megtalálásának körülményeit, többek közt azzal a fontos információval, hogy nem a sonka és a sajt mennyisége a korlátozó.

Következzék a b) feladat megoldása!

Most nem a mennyiség optimalizálása a cél, hanem a bevételé, ez kerül F9-be. Ezt leszámítva azonban ugyanúgy kell megoldani a feladatot, mint előbb.

A c)-ben egy kicsit már más jellegű a feladat, mint amilyen az előbbi volt. Egyrészről most minimális értéket keresünk, másrészről pedig egy új feltétel is adódik: mindenkinek jusson legalább egy szendvics.

Valójában még egy dologra is figyelni kellene: ne lehessen negatív számú szendvicset megadni. Mivel a bevétel minimalizálásáról van szó, ennek figyelembe vétele nélkül a megoldás a következő lenne: -43db sonkás szendvics, 57db sajtos szendvics és így 47Ft bevétel, ami nyilván nem egy életszerű megoldás. Az ok, amiért mégsem kell külön kikötni a szendvicsek számának nem negatív voltát, az egy kis jelölőnégyzet a Solver ablakában, ami alapértelmezetten ki van pipálva: "nem korlátozott változók nem negatívvá tétele".

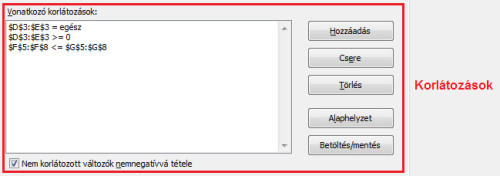A kép (nagyobb változata) külön ablakban is megtekinthető.74_full.jpg74. ábra: A jelölőnégyzet használata sok munkától megkímél minket.

A d) feladatban csupán az az újdonság, hogy a cél most nem valamiféle minimum- vagy maximum-optimalizálás, hanem egy konkrét érték általi visszafejtés. Igazából egy ugyanolyan visszakeresésről van szó, mint amit célérték-keresésnél is szoktunk csinálni, csak éppen az eddigi feltételek megtartása mellett:

Láttuk, hogy mekkora segítség lehet számunkra ez az eszköz, és azt is, hogy a táblázat elrendezésének kitalálását követően már egyszerű dolgunk van. Ennél bonyolultabb feladatoknál azonban jó résen lenni, és olykor esetleg felülbírálni a program működését, mert az sok esetben nem elég determinisztikus. A következő példa ezt mutatja be.

Egy verseny regionális fordulójának beosztását kell elkészíteni, az utazási költség minimalizálása mellett.

Adott:

• az iskolák neve és az onnan továbbjutók száma,
• a vizsgaközpontok (A, B, C és D) és maximális befogadóképességük,
• az egyes iskolák és a négy vizsgaközpont közti utazások költsége

Kell:

• a beosztás (melyik iskola tanulói melyik vizsgahelyre menjenek, figyelembe véve azok befogadóképességét),
• az összes utazási költség.

Mindezt tehát úgy kell megadni, hogy "ne szegjük meg a szabályokat", és az összes útiköltség a lehető legkevesebb legyen.

A feladat semmit nem ír arról, hogy ehhez a Solvert kellene használni, így aki nem ismeri ezt a lehetőséget, nagy valószínűséggel neki sem tud fogni a feladatnak. Sok esetben lehetne kézzel is próbálgatni, ennél a konkrét példánál azonban 4¹³ lehetőséget kellene megvizsgálni a férőhelyek figyelembevétele, illetve a költség minimalizálása szempontjából, amire nem hinném, hogy bárki szívesen vállalkozik (arról nem is beszélve, hogy még ha meg is találná a jó megoldást, akkor se sok pontot kapna a feladatra).

Elsőként importálni kell az adatokat, és valamilyen formában elrendezni őket a munkalapon. Utána át kell gondolni, milyen feltételeknek is kell megfelelni:

• a) Minden vizsgahelyre maximum a férőhellyel megegyező számú diákot osszunk be.
• b) Ugyanazon iskola tanulói ugyanazon vizsgahelyre legyenek besorolva.

Ezt követően arra van szükség, hogy a táblázat elrendezésével, képletek használatával ezeket olyan formában fogalmazzuk meg, amit "a Solver is megért". Ne feledjük, hogy csak a következő típusú feltételek adhatóak meg:

• Egy tartomány minden cellája legyen ≤, = vagy ≥, mint valamilyen általunk megadott értékek vagy cellák értékei.
• Egy tartomány minden cellája legyen egész.
• Egy tartomány minden cellája legyen 0 vagy 1.
• Egy tartomány minden cellája legyen egyedi.

Most jön egy kis okoskodás: "hogyan lehetne az előbb felsorolt feltételekkel megfogalmazni az a)-ban és b)-ben leírtakat?". Ezt kitalálni nem egyszerű. A következő képen a táblázat egy olyan elrendezése található, mely lehetővé teszi a feltételek megfogalmazását a következőképpen:

• a) $O$16:$R$16<=$H$22:$K$22
• b) $H$3:$K$15=bináris és $L$3:$L$15=1

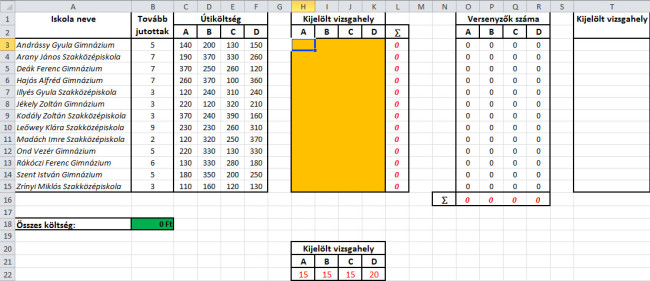A kép (nagyobb változata) külön ablakban is megtekinthető.75_full.jpg75. ábra: Az üres táblázat egy lehetséges elkészítése.

• Készítsük el a táblázatot a képnek megfelelően! A sárga tartományt kell a kívántaknak megfelelően kitölteni, a zöld cellában található az eredmény, a pirosakat pedig értelemszerűen, a megadott sárga mezők függvényében, képlettel számítjuk ki.
• Indítsuk el a Solvert (Adatok fül), és állítsuk be a következőképp:

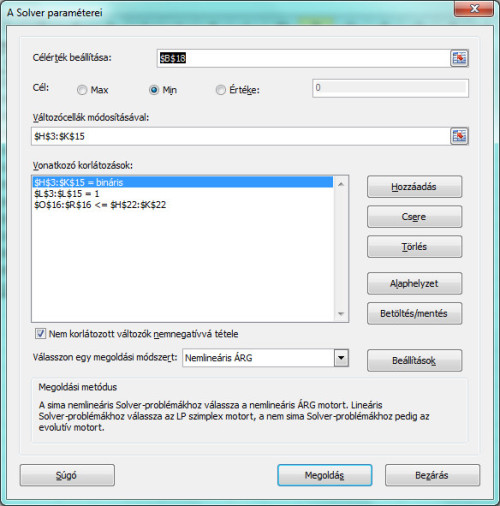A kép (nagyobb változata) külön ablakban is megtekinthető.76_full.jpg76. ábra: A célcella, a célérték, a módosuló cellák, valamint a korlátozások megadása.

A keresés jó ideig is eltarthat, majd nagy eséllyel a következő ablakot kapjuk:

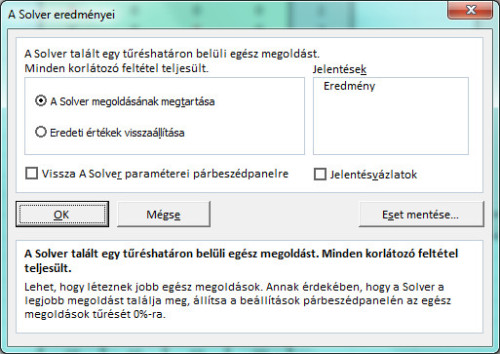A kép (nagyobb változata) külön ablakban is megtekinthető.77_full.jpg77. ábra: Úgy tűnik, nem is olyan biztos, hogy jó megoldást találtunk.

Az egész megoldások tűrését valóban célszerű nullára állítani, különben lehetséges, hogy egészek helyett csak egészekhez közeli értékekkel tölti fel a program a módosuló cellákat.

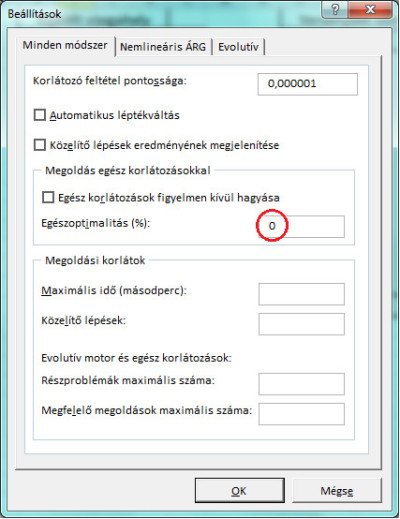A kép (nagyobb változata) külön ablakban is megtekinthető.78_full.jpg78. ábra: A Solver beállításai.

• Végezzük el az előbb említett beállítást, és futtassuk le újra a keresést!

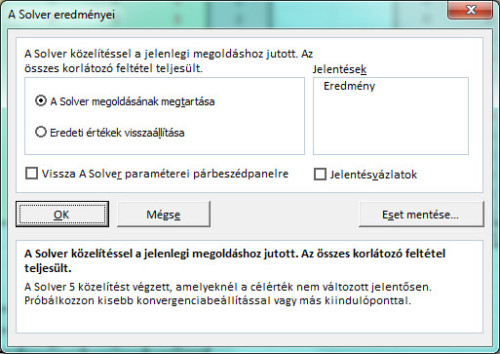A kép (nagyobb változata) külön ablakban is megtekinthető.79_full.jpg79. ábra: A beállítást követően se sokat javult a helyzet.

Habár javult a helyzet, és jobb megoldást kaptunk, mint előbb, még ez sem az igazi. Ha azonban még egyszer lefuttatjuk, jó eséllyel megkapjuk végre az optimális beosztást, mellyel az utazási költség mindössze 10530Ft lesz:

• Futtassuk ismét a Solvert, még mindig az eddigi beállításokkal!

A kép (nagyobb változata) külön ablakban is megtekinthető.80_full.jpg80. ábra: A Solver megtalálta a megoldást.

Az eddigi tortúrából egyértelműen megállapíthatjuk, hogy ez a feladat túl nagy falat a Solvernek, hiszen már elsőre meg kellett volna találnia a megoldást. Tapasztalataim szerint az Excel bizonyos verziói akár még arra is hajlamosak, hogy egyáltalán nem adnak megoldást (hacsak nem adunk meg kézzel "pár" kezdő értéket, megkönnyítve ezzel a dolgát). Sőt, olykor az is előfordulhat, hogy hiába állítjuk az egészoptimalitást 0%-ra, mégsem egészeket kapunk.

Ugyanezt a feladatot a LibreOffice Calcja kifogástalanul megoldja. A Solver funkciót teljes egészében megvalósító Megoldó pillanatok alatt megtalálja az optimális beosztást, amennyiben a LibreOffice lineáris megoldóprogramot választjuk a beállításokban (nem ez az alapértelmezett). Ebben az esetben ezért érdemesebb lehet ezt használni.

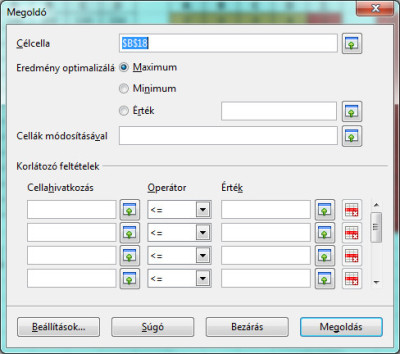A kép (nagyobb változata) külön ablakban is megtekinthető.81_full.jpg81. ábra: A Calc Megoldó nevű funkciójának ablaka.

Vissza a tartalomjegyzékhez