Tömb alatt Excelben egy téglalap alakú tartományt értünk. Ha az elemei egyetlen sorban vagy oszlopban helyezkednek el, akkor egydimenziós tömbnek, különben kétdimenziós tömbnek hívjuk. A tömbképletek - más néven CSE típusú képletek - olyan Excel-függvényeket tartalmazó képletek, melyeknek minden "bemenete" egy-egy tömb. Gyakran "fiktív" tömböket gyártanak működésük közben, melyekkel további számításokat végezhetünk, anélkül, hogy azokat valóban létrehoznánk a munkalapon. A "kimenet" lehet csak egy cella (egycellás képlet) vagy akár egy nagyobb tömb is (többcellás képlet). A képlet jóváhagyásához mindkét esetben a Ctrl+Shift+Enter gombok egyszerre történő lenyomására van szükség. Egy tömbképletet tartalmazó cellára kattintva a képlet kapcsos zárójelek közt jelenik meg a szerkesztőlécen, ez segíti gyors felismerésüket.
Használatukkal egyszerűsödhetnek bonyolult képleteink, és a segédcellák használata is kiküszöbölhetővé válhat. Előnye továbbá, hogy a többcellás képlet átírására csak egyszer van szükség, míg egy hagyományos képlet megváltozása esetén újra kell másolni azt, hogy a tömb összes érintett cellájában megváltozzon a képlet.
Működésüket először pár olyan feladat révén ismertetem, melyek megoldására ritkán választunk tömbképletet. Nem szeretném ugyanis egyből nehéz példával kezdeni, és ezzel esetleg elijeszteni azokat, akik korábban egyáltalán nem foglalkoztak még ezzel a lehetőséggel.
30. példa: Tömbképlet
Adott egy 20 soros táblázat fejléccel, A és B oszlopában tetszőleges számokkal: az A1:B21 tartomány.
a) Szorozzuk össze az A és B oszlopok értékeit E-be!
A feladatot eddig egy alkalmas képlet előállításával, majd annak másolásával oldottuk meg: E2=A2*B2. Most lássuk, hogyan oldható meg a feladat tömbképlettel!
A feladat tehát tömbképlettel is könnyedén megoldható, csak arra kell vigyázni, hogy a bemeneti tömbök és a kijelölt tartomány mind egyforma nagyságúak legyenek, hiszen tömbkimenetű képletről van szó.
Ha az utolsó lépésben Shift+Entert ütnénk, természetesen ugyanúgy megkapnánk a megoldást, csak a hagyományos módon. Szó sincs tehát arról, hogy egy ilyen feladatnál indokolt lenne tömbképletet használni.
30. példa: Tömbképlet
b) Adjuk meg a K2:K21 tartományba az A, illetve B oszlop adott elempárjai közül a maximumot!
A feladat természetesen most is megoldható hagyományos módszerrel, méghozzá egyszerűbben: =MAX(A2;B2).
A feladat tömbképletre való átírása most már egy kicsit elgondolkodtatóbb, hiszen a =MAX(A2:A21;B2:B21) képlet az összes (40db) elem egyetlen maximumát adja vissza. Ahhoz, hogy egy egész tömböt töltsünk fel a soronként meghatározott maximummal, HA() függvény használatára van szükség.
30. példa: Tömbképlet
c) Számoljuk össze az A2:A21 tartomány 5-nél nagyobb elemeit!
A kimenet most nem egy tömb lesz, mint az előző két példában, hanem egyetlen cella. Ezelőtt a feladatot így oldottuk meg: =DARABTELI(A2:A21;">5"), vagy esetleg AB.DARAB() függvénnyel. Oldjuk meg most tömbképlettel!
A következő történik: a HA() függvény az A oszlop minden egyes eleméről eldönti, hogy igaz-e rá a feltétel. Így minden elemhez hozzárendeljük az 1 és 0 számok valamelyikét, a feltétel igazságtartalmától függően. Keletkezik tehát egy 20 nagyságú "fiktív" tömb, melynek elemeit a SZUM() függvény összegzi.
A programozni tanulók számára a tömbképletek megértése valószínűleg sokkal könnyebben megy. Érdemesnek találom a feladatok vektorokkal(/mátrixokkal) történő lekódolását a tömbképletek tanításakor, hogy a diákok meglássák az analógiát, és a már meglévő tudásukra építve, könnyebben sajátítsák el az anyagot.
Akinek nehezen megy a leírtak elképzelése, és programozni sem tanult, nyugodtan készítse el előbb ezeket a "köztes", "fiktív" tömböket, hogy lássa, miknek az összegét veszi a SZUM() függvény. Például a =HA(A2:A21>5;1;0) képlet, egy 20 elemű oszloptartományon állva, Ctrl+Shift+Enterrel elfogadva egy ilyen tömböt generál.
Habár ritkán van rá szükség, de tömbképletek esetén is előfordulhat, hogy másolni szeretnénk őket valamilyen irányba (tipikusan egyetlen cellát visszaadó tömbképleteknél). Ekkor a relatív és abszolút hivatkozások beállítása a szokásos módon történik.
30. példa: Tömbképlet
d): Adjuk össze rendre A és B elemeit, majd vegyük az összegek szorzatát!
Ha a feladat a szorzatpárok összegét kérné, a SZORZATÖSSZEG() függvény a segítségünkre lenne. Alkalmas képlet híján a feladatot régi eszközeinkkel csak úgy tudjuk megoldani, hogy egy segédoszlopban kiszámoljuk az összegeket, majd a segédoszlop elemeit összeadjuk SZUM() függvénnyel. Ezzel azonban 20 darab segédcella használatára van szükség! Most már tehát tényleg indokolttá vált, hogy a feladatot tömbképlettel oldjuk meg, hiszen így nincs szükség segédcellákra.
Nem csak a segédcellák használatát kerültük el, de ez a megoldás sokkal egyszerűbb, és gyorsabban kivitelezhető is.
30. példa: Tömbképlet
e): Add meg, hány egyedi elem van az A tömbben!
Ehhez a korábbi módszerekkel a legtöbben úgy fognak neki, hogy létrehoznak egy tömböt, ami minden egyes sorában azt a számot tartalmazza, amennyi az adott tömb megfelelő sorában lévő elem előfordulása. Végül ebben a tömbben kell megszámolni, hogy hány darab 1-es szerepel:
=DARABTELI($A$2:$A$21;A2) függvénymásolással pl. I31:I50-be, majd =DARABTELI(I31:I50;1).
Tömbképlet használatával létrehozhatjuk ezt a köztes tömböt anélkül is, hogy az a munkalapon ténylegesen helyet foglalna. A képlet működésének megértéséhez azonban azt javaslom, hogy tömbképlet segítségével ugyan, de mégiscsak helyezzük el ezt a tömböt a munkalapon (később persze törölni fogjunk).
Egy kicsit talán furcsa, hogy a DARABTELI() függvény második argumentumában, feltételként egy tömb található, ráadásul ugyanaz, ami tartományként is szerepel, de valójában nem olyan nehéz elképzelni, mi is történik. A kijelölt tartományt töltjük fel számokkal, mégpedig pont ugyanazzal a módszerrel, mint az előbb. A tömbünk első cellájába =DARABTELI(A2:A21;A2) kerül, a másodikba =DARABTELI(A2:A21;A3) és így tovább.
Nincs más hátra, mint összeszámolni, hány darab 1-es van ebben a tömbben, de most már a tömb "fiktív" megvalósítása mellett tesszük ezt.
Elsőre talán nem érthető, miért nem működik ez a képlet. A magyarázat az, hogy a külső DARABTELI() függvény első paramétere nem egy tartomány, hanem egy szám: például =DARABTELI(DARABTELI(A2:A21;A2);1) = =DARABTELI(5;1).
A megoldáshoz egy kicsit korrigálni kell előbbi gondolatmenetünkön:
31. példa: Nemes 2009-2010 3. forduló, 5/D (Holdak)
A feladat és megoldása szerepel az Adatbázis-függvények című alfejezetben is (29. példa), ott az AB.MIN() és AB.MAX() függvényeket használtuk. Most ezeket cseréljük tömbképletekre, hogy egyáltalán ne kelljen segédcellákat használni.
A módszer talán már ismerős: készítünk egy tömböt, ami a megfelelő helyeken (tehát abban a sorban, ahol a megadott név szerepel mint felfedező) az ahhoz tartozó évszámot tartalmazza, a többi helyen pedig 0-t. Ennek a tömbnek kell a maximumát és a minimumát vennünk, hogy megkapjuk a kívánt két évszámot. Ehhez természetesen MAX(), illetve MIN() függvényeket fogunk használni.
Ezzel megadtuk a felfedezőhöz tartozó évszámok legnagyobbikát, feltéve, hogy van ilyen nevű felfedező (ha nincs, az eredmény nulla lesz). Ez elsőre egyszerűnek tűnhet, de azért át kell gondolnunk, miért is adhattunk meg a HA() függvény harmadik argumentumában nullát: mert ennél úgyis minden elem nagyobb. Ha nem tudnánk biztosan, hogy csak pozitív számok vannak a felfedezés événél megadva, már nem tehetnénk ezt meg.
Kérdés, hogy akkor mennyit adjunk meg a MIN() függvény esetén? Nyilván, a nulla nem lesz jó, hiszen akkor minden esetben az lenne a minimum. Egy olyan nagy számra van most szükségünk, aminél biztosan kisebb minden évszám: legyen például 10000!
Kihasználva, hogy a HA() függvény harmadik argumentuma nem kötelező, azt is megtehetjük, hogy egyszerűen elhagyjuk azt. Ilyenkor a képzeletbeli tömbünk azon soraiba, ahol nem teljesült a feltétel, HAMIS értékek kerülnek, és így nem zavarják a minimum-, illetve maximumszámítást.
Ezzel meghatároztuk a két évszámot. Ezek összeépítése a teljes választ szolgáltató képlettel nem nehéz, de amikor az adatbázis-függvényeket lecseréljük a tömbképletekre, és megpróbáljuk azt a szokásos módon érvényesíteni, a következő hibaüzenetet kapjuk:
![Az Excel hibaüzenete: "Tömbképletek nem szerepelhetnek egyesített cellákban."](kepek/68_w350.jpg "Az Excel hibaüzenete: "Tömbképletek nem szerepelhetnek egyesített cellákban."")
68_full.jpg68. ábra: A feladat egyesített cellába kéri az eredményt, de úgy tűnik, ilyet nem lehet.A megoldás a következő: előbb elkészítjük a teljes képletet az összevonandó cellák egyikébe (hiszen ezt engedi), és csak ezt követően vonjuk össze a cellákat.
32. példa: OKTV 2010-2011 1. forduló, 5/I (Tisztavatás)
Adott egy tisztek végzési adatait tartalmazó táblázat, többek közt a következő oszlopokkal: Név (A), Nem (B), Avatás éve (D), Kora az avatáskor (G), Szak (I), Tanulmányi átlaga (E).
A feladat, hogy megadjuk az olyan tisztek tanulmányi eredményének átlagát, akikre igazak az alábbi állítások:
A feladat könnyedén megoldható adatbázis-függvénnyel, a következő kritériumtáblázattal:
69_full.jpg69. ábra: AB.ÁTLAG() függvény esetén így néz ki a kritériumtáblázat.Ha azt szeretnénk, hogy egyáltalán ne legyen segédcella, tömbképlet használatára van szükség. Ez már elég összetett lesz, és a feladat ki sem köti, hogy nem szabad segédcellákat használni, mégis megmutatnám a megoldást. A módszer egyébként az eddig ismertettek továbbfejlesztése.
Ne feledjük, hogy HA() függvény esetén nem lehet helyettesítő karaktereket használni, ezért kellett a SZÁM() és a SZÖVEG.KERES() függvényeket egymásba ágyazni. Így a tömb egy eleme akkor lesz 1, ha az annyiadik sorban lévő szak megnevezése tartalmazza a "mérnök" kifejezést.
Azt akarjuk, hogy az összes feltétel teljesüljön. Ez pontosan akkor következik be egy sorra, ha az előbbi négy tömb mindegyikének 1 áll ebben a sorában. Másképpen: ahol a négy tömb megfelelő elemeinek szorzata 1, ott teljesült a feltétel.
A szorzattömb elemeinek összege így pont a darabszámot adja ki, vagyis hogy hány ilyen tiszt végzett.
Ezzel kell majd elosztani a megfelelő átlagok összegét. Utóbbi kiszámolására a módszer az eddigiekhez hasonló, de az átlagokat tartalmazó tömböt is be kell vennünk a szorzatba. Végül ennek a tömbnek is össze kell adni az elemeit.
Ha nincs a feltételeknek megfelelő diák, a cellában megjelenik a #ZÉRÓOSZTÓ! figyelmeztetés, csakúgy, mint az =AB.ÁTLAG() függvény használatakor.
Ez már egy eléggé elgondolkodtató példa volt. A nehézséget az is okozta, hogy tömbképleteknél nincs lehetőség logikai függvények használatára, mert azok nem tömböt, hanem egyetlen IGAZ/HAMIS értéket adnak vissza. Helyettük matematikai műveleteket kell használni. Előbb például szorzással váltottuk ki az ÉS kapcsolatot.
Nehezebb lenne a dolgunk, ha a feladatot VAGY kapcsolattal kellene megoldani. Arra még talán magától rájön, aki matematikában jártasabb, hogy a kulcs a négy tömb összeadása lesz, de azt is meg kell gondolni, mit kezdünk az 1-nél nagyobb összegekkel.
Az eddigi példákban a bemenet mindig egydimenziós tömb volt. Többdimenziós tömbökkel például mátrixműveleteknél találkozik az ember, ezek használatára, illetve az eddig leírtak összegzésére ajánlom a Tombkeplet.xlsx példafájlt.
Az eddigi példákban olyan függvényeket használtunk, melyeket hagyományos képletekben is gyakran használunk. Az Excel azonban tartalmaz pár olyan beépített függvényt is, amit inkább csak tömbképletként érdemes használni. Ezek közül a legismertebb a GYAKORISÁG(), mely használatára a versenyeken és a mindennapokban is gyakran szükség van.
33. példa: Nemes 2010-2011 3. forduló, 4/E (Eszmei érték)
Védett növények adatait tartalmazó táblázattal dolgozunk.
A példaválasztás nem véletlen, GYAKORISÁG() függvényre lesz szükségünk.
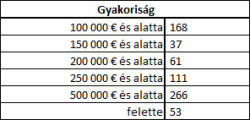70_full.jpg70. ábra: Az egyes értékhatárok, és a hozzájuk tartozó fajok száma.Ki lehetne egyébként DARABTELI() függvényekkel is számolni az egyes példányszámokat, de ahhoz, hogy egy növényt csak egy kategória esetén számoljunk meg, mindig ki kellene vonni a már kiszámolt értékeket. A megoldás így időigényes lenne, hiszen függvénymásolást nem tudnánk alkalmazni.
Itt az első argumentum a becsült összértékeket tartalmazó oszlop a táblázatban, a második pedig az imént készített tartomány. A függvényt természetesen Ctrl+Shift+Enterrel kell jóváhagyni. Az első szám, amit kaptunk, azon példányok száma, melyek becsült összértéke ≤100000. A következő szám azon példányok mennyiségét jelöli, amik összértéke >100000 és ≤150000 és így tovább. A kapott tömb utolsó eleme azon példányok számát jelöli, amik értéke még az utolsó megadott határt is meghaladta: >500000.
A függvény minden esetben így működik, ezért ügyelni kell a kijelölt cellák számára és a határok növekvő sorrendjére. Az Excel egyébként nem figyelmeztet, ha véletlenül kevés cellát jelöltünk ki, hanem egész egyszerűen csak azokat az értékeket számolja ki. Érdemes ezért mindig ellenőrizni, reális adatokat kaptunk-e, például az összegek összegzésével.
Elképzelhető olyan feladat is, ahol - az előző feladattól eltérően - diszkrét eseteket számolunk. Például, kigyűjtjük az összes létező becsült eszmei értéket, és megnézzük, melyik érték hányszor fordult elő. Ekkor a kapott példányszámok azt jelentik, hány olyan egyed van, ahol az eszmei érték pontosan annyi, mint a ="határokat=" megadó tartomány aktuális eleme. A függvény ugyanúgy helyesen fog működni, mint eddig, az utolsó kapott érték viszont szükségképpen nulla lesz. Emiatt bevett szokássá vált, hogy pont annyi cellát jelölnek ki, mint ahány határ van, csak azért, hogy a nulla ne legyen zavaró. Ez diszkrét eseteknél általában még nem jelent problémát, de ez a "lespórolás" okozhatja azt a típushibát, hogy sokaknál folytonos eseteknél is hiányzik az utolsó cella. Ezért pedagógusként nem tartom tanácsosnak a diszkrét esetek megoldásának elkülönítését a folytonos esetekétől: nem olyan zavaró ott az a nulla, mint amekkora gondot okozhat az utolsó cella lefelejtése folytonos eseteknél.
 |
 |
 |
| Készült az "Országos koordinációval a pedagógusképzés megújításáért” című TÁMOP-4.1.2.B.2-13/1-2013-0007 pályázat keretében. | ||
A tananyag az ELTESCORM keretrendszerrel készült